澳门金沙娱乐城官网-金沙官网

日前，北京理工大學物理學院張向東教授課題組，在拓撲電路研究方面取得重要進展。他們設計并制備出了一種新型空時電路，被稱作“拓撲空時電路”，相關工作以“Topolectrical space-time circuits”為題發表在Nature Communications上[Nat. Commun. 16, 198 (2025)]。北京理工大學物理學院張蔚暄研究員和博士生曹汶慧、錢龍為論文的共同第一作者，張向東教授為通訊作者。研究工作得到國家重點研發計劃和國家自然科學基金的資助。

周期性含時驅動是一種調控量子和經典系統的強有力手段，為突破傳統靜態系統的物理限制并實現新奇拓撲物態提供了全新的契機。近年來，研究人員在各種時變系統中揭示了豐富多樣的新奇物態，包括離散時間晶體、拓撲泵浦、光子時間晶體以及Floquet拓撲態等。尤其值得關注的是，近期理論上提出了具有(d+1)維空時平移對稱性的空時晶體。這一體系與傳統Floquet-Bloch系統顯著不同，后者的時間和空間平移對稱性是解耦的，而空時晶體則擁有不可分離的空時平移對稱性。進一步的研究表明，在(1+1)維和(2+1)維空時晶體中具有由和拓撲不變量刻畫的拓撲空時晶體物態。這一發現為拓撲物態的研究開辟了全新的視角。然而，由于拓撲空時晶體需要對空間和時間自由度進行全面而精準的調控，這使得在現有的量子和經典平臺上實驗實現面臨巨大挑戰。

拓撲電路作為研究拓撲物理的新型實驗平臺，展現出傳統量子材料和經典人工結構(如光學、聲學、力學、熱學等)所不具備的獨特優勢。首先，經典電路可以實現與空間維度和節點距離無關的非局域耦合，這為高維拓撲晶格結構、非歐幾里得拓撲態以及具有非阿貝爾耦合特性的拓撲態實驗研究提供了理想平臺。此外，經典電路擁有豐富多樣的有源和無源元件，包括不同規格的電容、電感、電阻、運算放大器、乘法器、憶阻器和二極管等，使得探索傳統材料難以實現的拓撲物理特性(如非互易耦合、多種非線性效應以及增益/損耗特性)成為可能。同時，低頻拓撲電路的設計理念還能夠直接推廣到集成電路芯片的設計，為開發具有特殊功能的新型電路芯片提供了重要思路。拓撲空時電路憑借其獨特的空時拓撲特性和動態調控能力，在無線電通信、超敏傳感和信息數據處理等領域具有潛在的應用前景。然而，如何實現對電路網絡中時間和空間自由度的協同調控，以構造出具有空時平移對稱性的新型拓撲電路，仍是亟待解決的關鍵科學問題。

研究亮點一：(1+1)維拓撲空時電路的構建和拓撲空時邊界態的實驗觀測。

研究人員首先對具有(1+1)維空時平移對稱性的晶格模型進行了系統研究，其哈密頓量形式為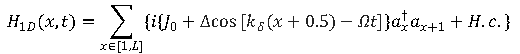，滿足空時平移對稱性和。基于空時平移對稱性，研究人員借助廣義Floquet-Bloch定理對準動量空間中系統的Floquet哈密頓量進行了對稱性分析。該系統具備廣義粒子-空穴對稱性，可以實現由拓撲不變量表征的拓撲邊界態。圖1a展示了系統在開邊界條件下的準能譜分布，其中顏色表示對應本征態的邊界局域強度。可以清晰看到在ε = ±0.5Ω附近存在邊界態(圖1b)。圖1c進一步展現了系統準能譜k_δ的變化。結果顯示，拓撲空時邊界態在k_δ ∈ [0.59π,1.41π]的范圍內出現，表明空時拓撲相變發生在k_δ = 0.59π和1.41π處。需要指出的是，該(1+1)維拓撲空時晶體的緊束縛晶格模型僅包含一個軌道(一個子格)，這不同于靜態和Floquet對應模型中常見的兩軌道最小拓撲模型。這種單軌道特性來源于頻率域擴展空時哈密頓量的獨特能帶結構。具體來說，在不同的Floquet扇區之間的對角能帶不僅表現出能量偏移，還在動量上呈現kδ的整數倍差異。因此，相鄰Floquet扇區中同一軌道的對角能帶在特定動量點處可以相交。當這些能帶通過時間調制耦合時，拓撲能隙便可打開。在傳統Floquet–Bloch系統中，要打開拓撲能隙至少需要兩軌道模型。拓撲空時晶體的單軌道性質可推廣至(d+1)維拓撲空時晶體。

進一步，研究人員設計并制備了(1+1)維拓撲空時電路，實現了對上述拓撲邊界態的實驗觀測。為了實現電路耦合的空時調制，他們設計了一種由外加信號控制的時變非互易電阻(圖1d)。通過調節不同電路節點之間控制信號的相位和頻率，可以構造出具有(1+1)維空時平移對稱性的電路網絡(圖1e)。實驗樣品的實物照片及細節放大圖顯示在圖1f中。研究人員測量了電路網絡的電壓動力學，并將其與理論仿真結果進行了對比(圖1g-h)。測量結果與仿真高度一致，傅里葉變換得到的頻譜在133.5Hz處顯示出拓撲邊界態的特征頻率(圖1i)。當頻率為133.5Hz時，傅里葉變換下的電壓分布呈現出強烈的邊界局域性(圖1k)；相比之下，體態頻率267Hz下的電壓分布則表現為空間擴展分布(圖1j)。這些結果清晰地證明，通過拓撲空時電路成功實現了(1+1)維拓撲空時邊界態。

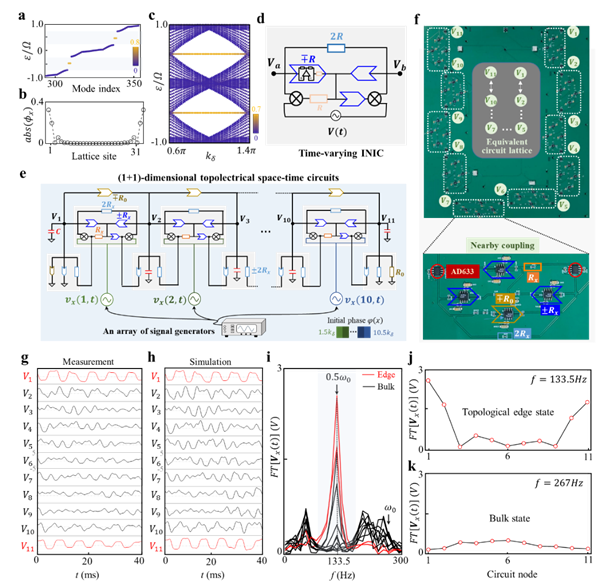
圖1. (1+1)維拓撲空時電路的理論和實驗結果。

研究亮點二：基于(2+1)維拓撲空時電路實現手性拓撲邊界態的實驗觀測

進一步，研究人員考慮(2+1)維拓撲空時晶體，其哈密頓量為，滿足空時平移對稱性和。類似于(1+1)維空時晶體，(2+1)維空時晶體也可以用準動量空間中的Floquet哈密頓量來描述。分析發現，ε = ±0.5Ω附近的低能量有效哈密頓量沒有時間反演、粒子空穴和手征對稱性，可以用拓撲不變量來表征。圖2a展示了系統在開邊界條件下的準能譜分布，其中顏色表示對應本征態的邊界局域強度。可以清晰看到，ε = ±0.5Ω附近存在拓撲空時邊界態(圖2c)。需要強調的是，ε = 0.5Ω和-0.5Ω附近的拓撲邊界態是由不同能量扇區單軌道Floquet能帶耦合得到，相鄰能量區間的拓撲空時邊界態色散滿足ε → ε+Ω和k_x → k_x + kδ^x(圖2b)。圖2d進一步展現了(2+1)維拓撲空時晶體的相圖,拓撲相變發生在kδ^x和kδ^y的絕對值接近π的區域。

最后，研究人員設計并制備了(2+1)維拓撲空時電路(圖2e-2f)，實現了對上述拓撲邊界態的實驗觀測。圖2g-2j顯示了不同時刻的電壓空間分布。可以看到初始電壓沿電路邊界單向傳播，展現了(2+1)維拓撲空時邊界態的手性行為。

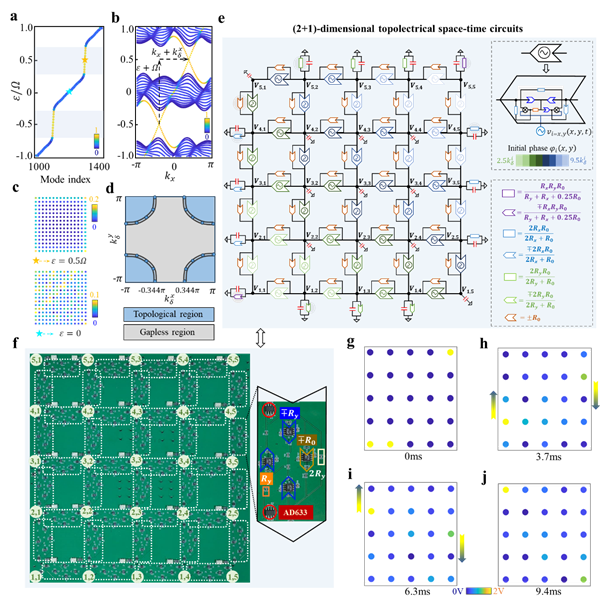
圖2. (2+1)維拓撲空時電路的理論和實驗結果。

研究亮點三：(3+1)維Weyl空時半金屬及拓撲空時電路實現。

研究人員對哈密頓量形式為的(3+1)維拓撲空時晶體進行了系統性研究。J_z是沿z軸的常數耦合，沿x和y軸的時變耦合為和，滿足離散空時平移對稱性。與(1+1)和(2+1)維拓撲空時晶體類似，(3+1)維空時晶體也可以用 Floquet哈密頓量H(k_x, k_y, k_z)來描述。當時變耦合較弱時，ε = -0.5Ω附近的低能有效哈密頓量與傳統系統的Weyl哈密頓量具有相同的形式。因此，可以通過調節系統參數，實現空時Weyl點。圖3a展示了Floquet哈密頓量的準能帶結構，可以看到空時Weyl點出現在ε = -0.42Ω和ε = -0.58Ω處。值得注意的是，Weyl點出現的位置與低能有效哈密頓量預測值基本匹配，只有k_z值由于其他能帶的存在略有偏差。此外，不同Floquet扇區中的空時Weyl點具有空時平移對稱性ε → ε+Ω和。空時Weyl點的存在還可以在開邊界結構中誘導表面狀態出現(圖3c)。這些表面態可以形成Fermi-arc,如圖3d所示。圖3e展示了開邊界條件下，(3+1)維拓撲空時晶體的準特能譜。圖3f-3g繪制了ε = -0.497Ω的Weyl表面態和ε = -0.41Ω的體態的空間分布。最后，研究人員設計并制備了(3+1)維拓撲空時電路(圖3h-i)，實現了對上述空時Weyl表面態的實驗觀測（圖3j-3m）。

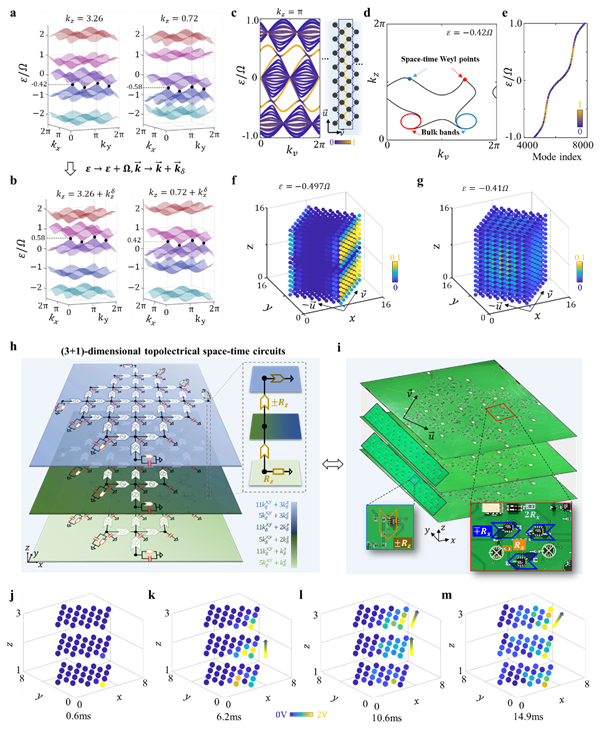
圖3. (3+1)維拓撲空時電路的理論和實驗結果。

該工作首次提出拓撲空時電路的概念，并實現了對(1+1)維、(2+1)維和(3+1)維拓撲空時物態的實驗觀測。與傳統Floquet-Bloch拓撲系統不同，空時平移對稱性使拓撲空時晶體具有單軌道特性。該工作為未來探索更加復雜的拓撲空時效應奠定了實驗基礎。另外，低頻拓撲空時電路的設計方法可以擴展到CMOS芯片領域，為設計新型拓撲空時電路芯片提供了重要參考。

文章鏈接：https://doi.org/10.1038/s41467-024-55425-1