北理工物理學院在弱拓撲絕緣體以及復合的外爾半金屬領域取得重要研究進展
發布日期:2016-05-23 供稿:物理學院
編輯:周格羽 審核:姚裕貴 閱讀次數:最近,北京理工大學物理學院量子功能材料設計與應用實驗室姚裕貴教授研究組(劉鋮鋮博士、周金健博士生、姚裕貴教授)和德州大學達拉斯分校的張帆博士合作提出了弱拓撲絕緣體和復合的外爾(Weyl)半金屬可以在一類動力學穩定和業已合成的范德瓦爾斯(van der Waals)材料-beta-Bi4X4(X=Br,I)中實現。相關研究成果發表在近期的《物理學評論快報》上(Phys. Rev. Lett. 116, 066801 (2016))。該工作得到了北理工校優青,校基礎基金以及國家自然科學基金委和科技部的資助。
以拓撲絕緣體為代表的一系列量子態的發現正在革新并深化了我們對量子材料的基本認識。這種基本認識和理解可能導致前所未有的技術應用優勢。比如,拓撲絕緣體中可控的量子相變以及受保護的自旋動量鎖定的表面態在Majorana基的拓撲量子計算中有著重要的應用前景。三維的拓撲絕緣體需要用四個拓撲指標來描述 (v0; v1,v2,v3)。如果v0不等于0,即為所謂的強拓撲絕緣體;如果v0=0,而v1,v2,v3 不全為零,則稱為弱拓撲絕緣體。強拓撲絕緣體具有奇數個Dirac表面態,而弱拓撲絕緣體具有偶數個Dirac表面態。值得指出的是,強、弱拓撲絕緣體是一同被理論首先預言出來的。很快,實驗上便證實和發現了若干個強拓撲絕緣體材料。該類拓撲絕緣體被研究的最多也最透徹。這得益于大多數的強拓撲絕緣體都是層狀材料。該結構特點使得實驗上可以很容易在解理面上觀察到強拓撲絕緣體的指紋-奇數個表面Dirac錐,而不需要特別的表面鈍化處理。然而,令人驚訝的是,到目前為止實驗上還沒有發現弱拓撲絕緣體。一個自然的想法是通過堆垛二維的拓撲絕緣體來得到弱拓撲絕緣體。該方法的最大問題是弱拓撲絕緣體的特征表面Dirac錐只能在側面而非解理面觀察到,而在其解理面(平行于堆垛平面)沒有特征表面態。我們知道非解理面難于獲得且不穩定,同時會具有大量的懸掛鍵,這些都給實驗驗證帶來了巨大的挑戰。因此,找到一個新的體系能夠在實驗上易于驗證且能夠便于研究弱拓撲絕緣體特有的新奇物性是迫切和重要的。
在前期研究該類二維大能隙拓撲絕緣體的工作基礎上(Nano Lett. 14,4767 (2014)),最近,北理工物理學院量子功能材料設計與應用實驗室劉鋮鋮博士、周金健博士生、姚裕貴教授和德州大學達拉斯分校的張帆博士合作提出了弱拓撲絕緣體可以在范德瓦爾斯(van der Waals)材料-beta-Bi4X4(X=Br,I)中實現并可以容易地被實驗驗證。如圖1所示,該類材料的基本構建單元是一維的原子鏈。垂直于該原子鏈方向的兩個晶面(100)和(001)都是解理面。本征的beta-Bi4Br4、beta-Bi4I4分別是弱拓撲絕緣體和強拓撲絕緣體。他們還發現單軸應變可以使得體系發生拓撲相變。在不同的應變區,可以得到強拓撲絕緣體、弱拓撲絕緣體以及普通的能帶絕緣體,如圖3所示。對于弱拓撲絕緣體,在(001) 解理面是沒有拓撲表面態的,而在(100) 解理面,出現了兩個各向異性的表面Dirac錐,見圖2。并且,當對該體系進行電荷摻雜時,可以發現該表面態發生了四次Lifshitz轉變。alpha-Bi4Br4、alpha-Bi4I4由于其元胞沿c方向長度加倍,相應的高對稱點都反帶兩次,所以都是拓撲平庸的能帶絕緣體。值得特別指出的是,如圖4所示,在從弱拓撲絕緣體到強拓撲絕緣體轉變的同時破缺體系的反演對稱性,會出現一個全新的Weyl半金屬相,即在兩個解理面都出現了費米弧(Fermi arc),但是只在(100) 解理面出現費米環(Fermi circle),我們稱之為復合的Weyl半金屬。
作為典型的弱拓撲絕緣體,該類范德瓦爾斯(van der Waals)材料-beta-Bi4X4(X=Br,I)為研究很多新穎的物理提供了一個理想的平臺。當體系在平均的意義上具有U(1), 時間反演以及平移對稱性時,弱拓撲絕緣體對于無序是穩定的。當破缺其中任一對稱性,都將會引入相應的新奇物理效應。如螺位錯以及臺階等拓撲缺陷的引入會破缺平移對稱性將會導致螺旋的邊界態。又如磁性的引入可以破缺時間反演對稱性會導致量子反常霍爾效應。再如與超導的鄰近耦合效應可以破缺U(1)對稱性從而導致帶有Majorana 零模的拓撲超導體。
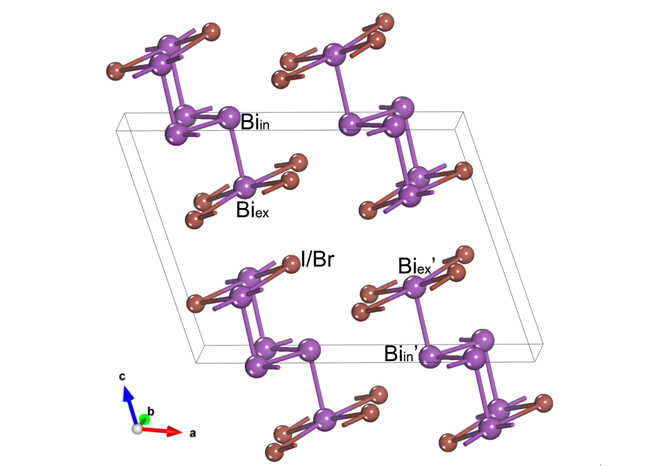
圖1晶體結構。體系關于(010)面具有鏡面反演同時具有空間反演對稱性。
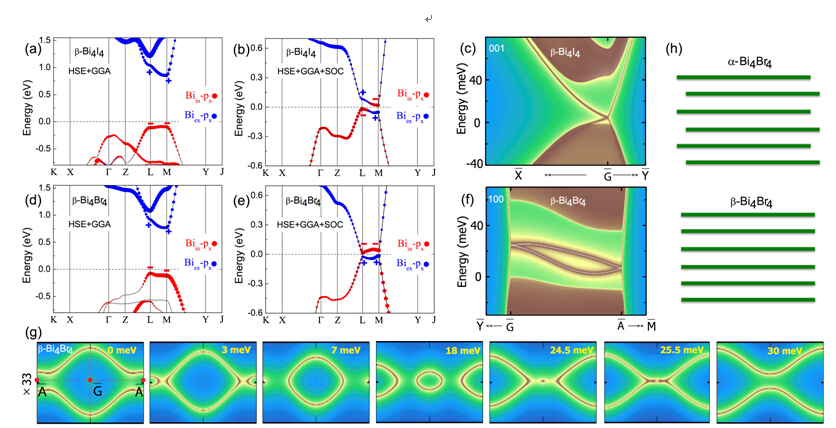
圖2電子結構。(a) (b) ?-Bi4I4有無自旋軌道耦合的能帶結構。(c) ?-Bi4I4的(001)表面態。(d)(e) ?-Bi4Br4有無自旋軌道耦合的能帶結構。(f) ?-Bi4Br4的(100)表面態。(g) ?-Bi4Br4的(001)表面態的Lifshitz轉變。(h) / ?-Bi4Br4的堆垛示意圖。
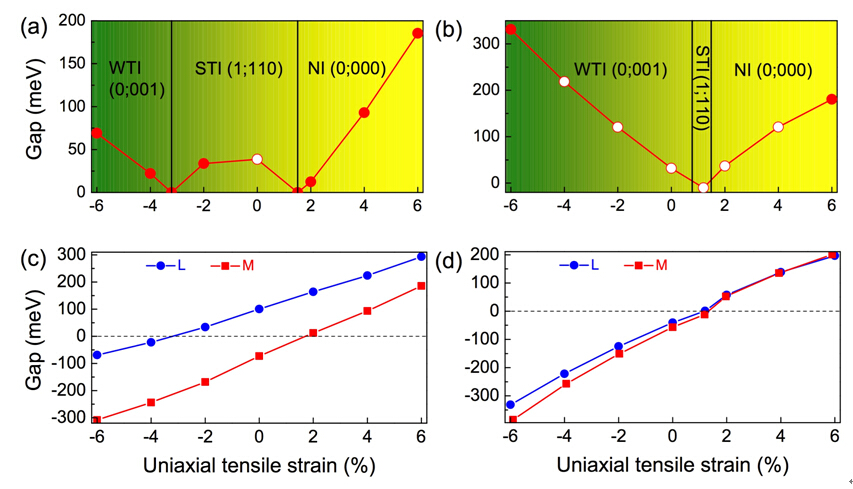
圖3單軸應力導致的拓撲相變。
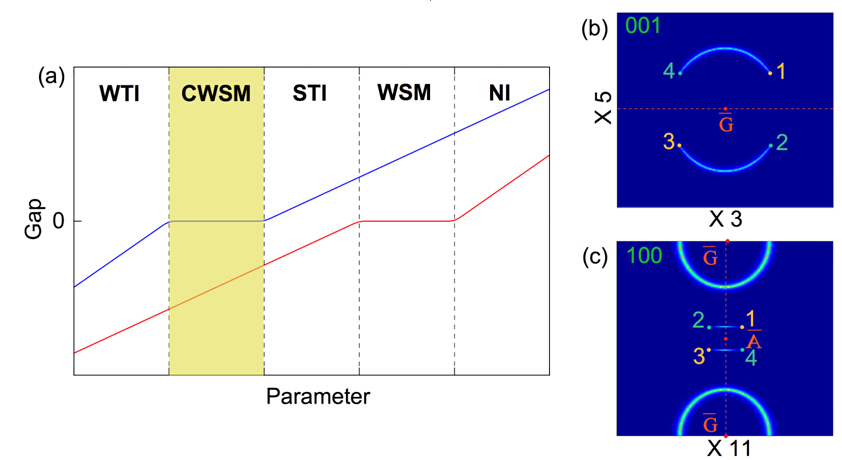
圖4(a)相圖。強弱拓撲絕緣體相變時可出現我們提出的復合Weyl 半金屬。而強拓撲絕緣體和能帶絕緣體的拓撲相變時可出現通常的Weyl 半金屬。(b) 復合Weyl 半金屬在(001)解理面的Fermi arc。(c) 復合Weyl 半金屬在(100)解理面共存的Fermi arc以及Fermi circle。
分享到:
