澳门金沙娱乐城官网-金沙官网

近日，北京理工大學物理學院張向東教授課題組通過設計四階簡并奇異點，實現了拓撲保護的糾纏態手性開關。相關成果以“Topologically Protected Entanglement Switching Around Exceptional Points”為題發表在Light: Science & Applications期刊[Light Sci. Appl. 13, 167 (2024)]上。該研究工作得到了國家自然科學基金委的大力支持。北京理工大學物理學院湯贊博士、陳天副教授為該論文的共同第一作者，北京理工大學物理學院陳天副教授、張向東教授為論文共同通訊作者，北京理工大學物理學院博士生唐杏也為該工作做出了重要貢獻。

量子糾纏作為量子力學的核心，展示了不可分性和非局域性，已經在各種物理系統中被實驗證實。然而，它容易受到環境的影響，經常出現退相干現象。如何進行魯棒的糾纏操作對量子信息的應用至關重要。最近的研究表明，拓撲學與量子態的結合能為解決這一問題帶來希望，包括拓撲量子光學界面，拓撲量子光源，拓撲保護雙光子量子關聯，糾纏光子的拓撲魯棒傳輸等。問題在于，在經過這些已報道的拓撲保護操作之后，糾纏態的保真度變得非常低。雖然使用逆設計方法可以提高糾纏態的轉換效率，但不同糾纏態之間的轉換需要設計各種參數才能實現。此外，信號還會散射到非拓撲保護信道，導致糾纏態轉換的重大損失。因此，如何實現高保真的魯棒糾纏態操作仍是未能解決好的問題。

另一方面，奇異點作為非厄米系統中的簡并點，其研究已引起越來越多的關注。這是因為奇異點周圍或附近相變的突變性已被證明會導致許多有趣的現象，如拓撲模式和能量轉移、激光模式選擇、奇異點增強模式分裂、損耗誘導透明度、單向隱形等。這些現象不僅在經典系統中進行了觀察，而且在量子體系中也得到了研究。問題是能否或如何利用奇異點的特性實現糾纏態的魯棒性操作？

研究亮點之一：構造四階簡并奇異點實現量子糾纏態的非對稱轉化

在以往的許多研究中，奇異點的動態環繞是用哈密頓量算符來描述的。在該工作中，研究團隊提供了另一種描述此類問題的方法，即利用非厄米量子行走演化算符。如圖 1a 所示，作為輸入態的兩個糾纏粒子（紅色和灰色球體）入射到由多個算符組成的陣列上。兩個糾纏粒子在算符陣列中沿著不同的路徑演化，輸出的糾纏態可以表示為。每個演化步驟都由量子行走算子，以及前后控制算子和組成。以第一步演化算符為例，單步演化過程可分為三個階段。首先，兩個粒子都受到算符的作用。接下來，紅色粒子進入單位矩陣模塊，而灰色粒子進入由多個算符組成的量子行走模塊。這里是旋轉算符。是相位平移算符，是增益損耗算符，是對稱性破壞算符。當兩個粒子經過后，它們都會受到算符的作用。之后，作用于兩個粒子的每一步演化算符都遵循類似的三階段過程，不同之處在于演化過程中的參數發生了變化。

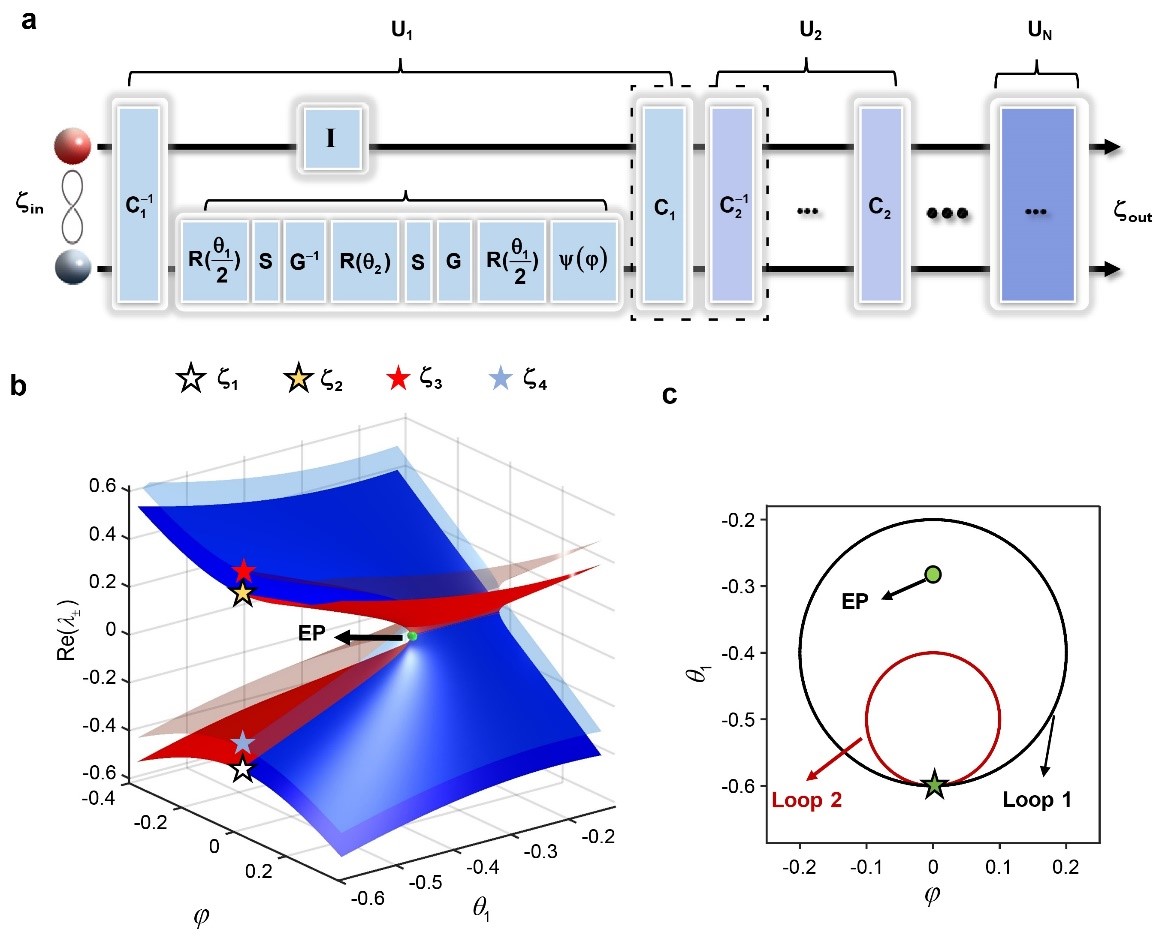
圖1. 構造非厄米量子行走實現糾纏態環繞奇異點的動態演化

以參數和為變量，研究團隊通過求解特征方程得到特征值 ，這里是演化系統的準能量，代表演化算符的四個特征態。圖 1b 顯示了準能量的實部，四個能量面被分為兩組，每組包含兩個簡并黎曼能量面。一個由綠色球體表示孤立的奇異點存在于這些面的分支點處。與之前研究中黎曼面不同的地方是這里每一個能量特征值對應兩個不同的特征態，因此可以看成存在著兩個重疊的黎曼面。研究人員發現，通過適當選擇參數，圖 1a 中描述的糾纏態演化過程可以表現出環繞奇異點的行為。如圖 1c 所示，首先選擇圖 1b 中星號標記作為起點，并選擇參數演化路徑為黑色Loop 1。接下來，將四個貝爾態，， 和作為系統的輸入態，便可以研究其演化過程。

四個輸出態的理論密度矩陣如圖 2 所示。圖 2e-2h 對應的是順時針變化的情況，而圖 2i-2l 對應的是逆時針變化的情況。為便于比較，圖 2a-2d 顯示了輸入狀態的密度矩陣。圖 2a-2d 中的白色、黃色、紅色和藍色星號與圖 1b 中標注的星號相對應，分別代表輸入態，，和。如圖 2e 和 2f 所示，當輸入態為和并順時針環繞奇異點時，演化的輸出結果都非常接近糾纏態。計算出的保真度F分別高達98.3% 和96.4%。相比之下，如果逆時針環繞奇異點時，輸出結果都非常接近糾纏態，且保真度一樣很高，見圖 2i 和 2j。這表明環繞奇異點可以實現糾纏態和糾纏態之間的非對稱轉換。對于在另一重疊黎曼面上和的演化也有類似的結果。上述研究表明，環繞奇異點可以實現四種糾纏態之間的非對稱轉換，即實現糾纏態的手性開關。轉換中的輸出糾纏態由環繞奇異點的方向決定，轉換效率非常高。這一現象可歸因于演化算符的四個特征態與四個輸入貝爾態之間的一致性。

圖2. 環繞四階簡并奇異點的糾纏態演化理論結果

研究亮點之二：基于非厄米量子行走實驗實現魯棒的糾纏態手性開關

研究人員構建的非厄米量子行走平臺如圖 3 所示，包括初態準備、演化過程和測量三個部分。這與圖 1a 中的理論方案相對應。在初態準備過程中，研究人員使用波長為400 nm的皮秒激光脈沖泵浦BBO晶體，通過 I 型參量下轉化產生 800 nm 波長的光子對。兩個粒子的量子態分別編碼在兩個光子的水平和垂直偏振態中。在實驗中，作為最大糾纏態的貝爾態被選為初始態。由于算符作用于四個貝爾態可以得到易于精確制備的輸入態，研究人員便通過半波片和四分之一波片來直接實現，然后將它們送入多步演化模塊中。

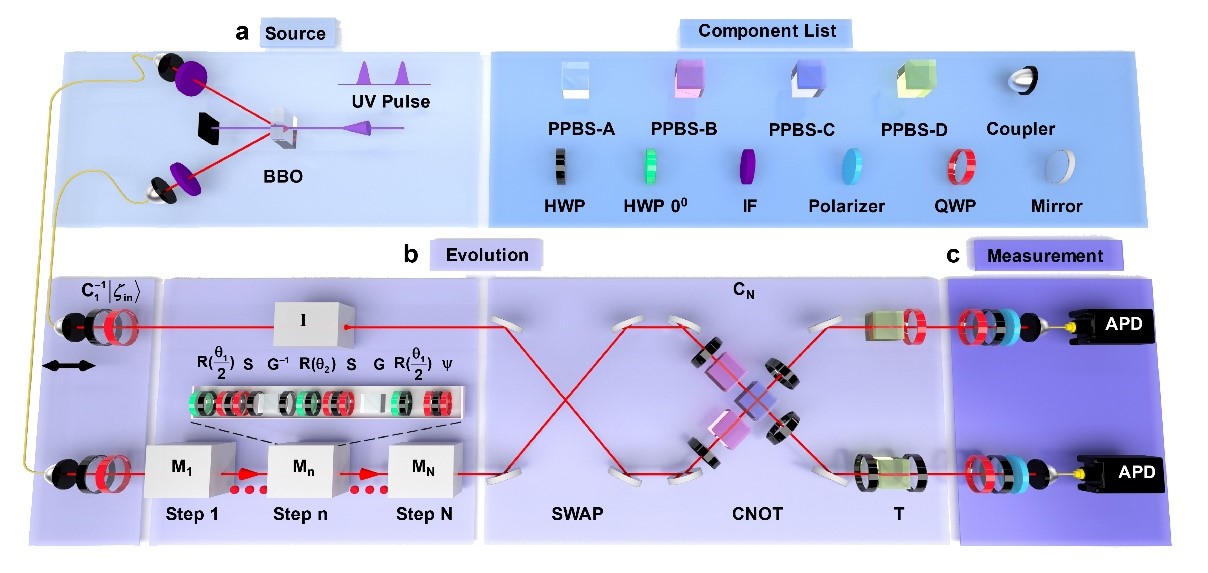
圖3. 拓撲保護糾纏態手性開關的實驗示意圖

在演化過程中，一個光子在自由空間傳播，另一個光子進入量子行走模塊。旋轉算符通過使用角度為零的綠色半波片和角度為的黑色半波片的組合來實現。兩個四分之一波片和一個半波片被一起用來實現條件相移算符S。對于增益-損失算符G可以用等效的增益-損失算符來實現。此外，為了實現對稱破壞算符，在每一步的末端都放置了四分之一波片和半波片的組合。對于最后一個操作，研究人員將其分解為 SWAP 門、CNOT門和算符 T 的乘積。在實驗中，SWAP 門可以通過使用鏡子交換上下光子來實現。CNOT 門是通過使用部分偏振分束器PPBS-B 和PPBS-C 的組合進行 Hong-Ou-Mandel 干涉來實現的。對于算符T，通過在上下路徑中放置了不同四分之一波片，半波片和部分偏振分束器的組合便可實現。

在兩個光子經過上述演化過程后，研究人員執行雙光子量子態層析來測量輸出態。16組測量基由四分之一波片，半波片和偏振片組成，對輸出態進行投影測量。有了這些投影測量結果，量子態層析就可以被完成并且輸出態的密度矩陣也能被重建。

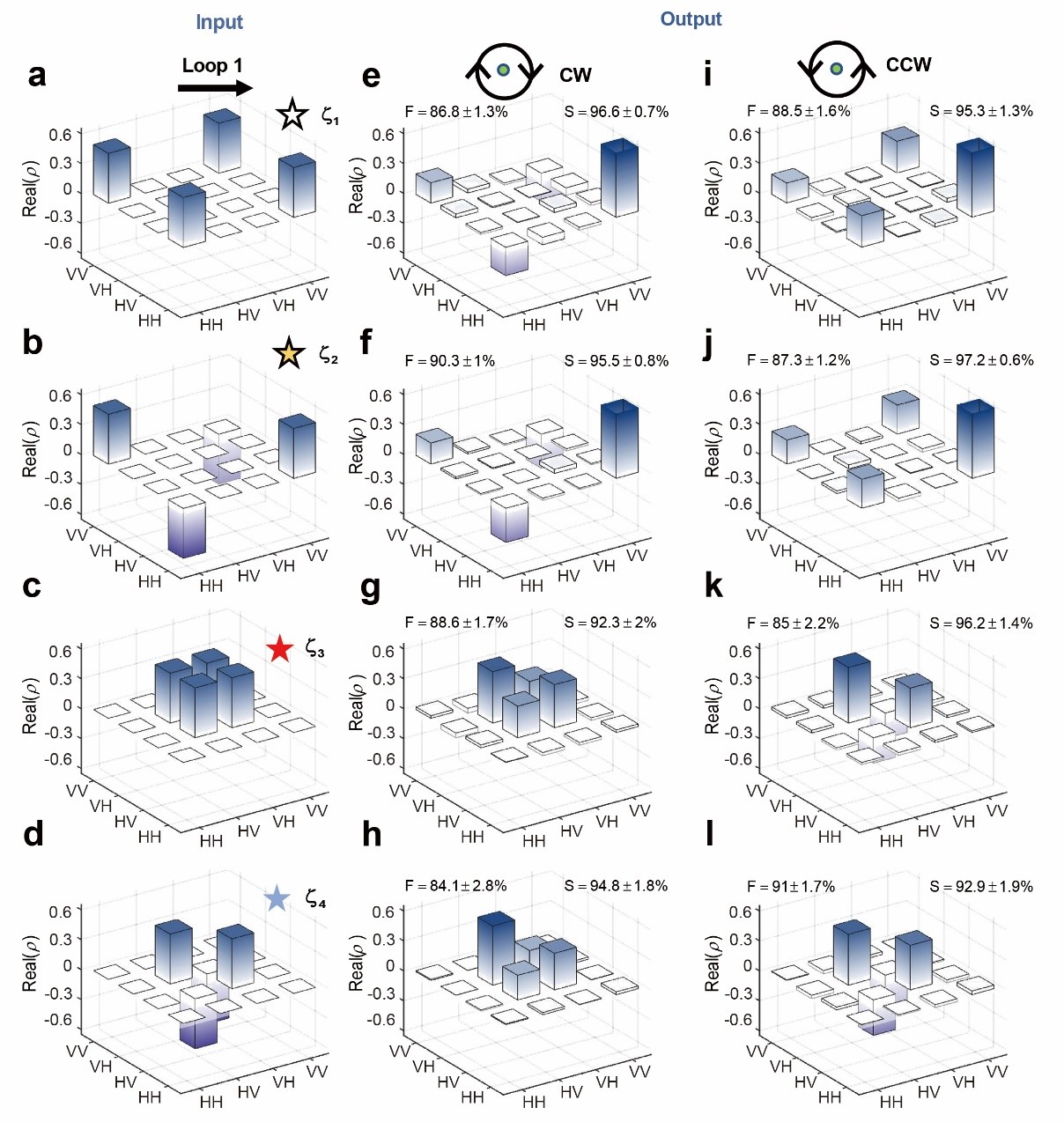
圖4. 環繞四階簡并奇異點的糾纏態演化實驗結果

輸出狀態的實驗結果如圖 4 所示。這些結果與圖 2 所示的理論結果基本相同。在實驗中，計算了輸出態與理想糾纏態之間的保真度，顯然可見所有保真度都達到 84% 或以上，表明輸出態非常接近理想糾纏態。由于實驗的總步數為 8 步，輸出態與理想糾纏態之間存在一些差異，但足以證明糾纏態的手性開關。研究人員還計算了理論結果與實驗結果的相似度S，可以看出，所有情況下的相似度都大于92%，表明實驗與理論之間的吻合度非常高。這意味著已經成功地通過實驗證明了四種貝爾態的手性開關這一現象。

此外，糾纏態開關的魯棒性也被實驗驗證了。在實驗中，研究人員在環繞路徑中引入了無序狀態，以觀察輸出糾纏態的變化。其中無序是通過給波片的旋轉角度添加小的隨機擾動來實現的，即路徑參數變為和。圖 5 顯示了十組擾動的平均結果。藍色柱子代表著沒有無序的情況下，輸出態與糾纏態之間的保真度，而灰色柱子代表有無序擾動時輸出態的保真度。圖 5a 顯示了順時針環繞奇異點的情況。可以看出，對于四種不同的輸入貝爾態，有擾動時的保真度與沒有擾動時相比變化不大，且都保持在0.8 以上。圖 5b 中逆時針環繞奇異點時也有類似的結果。這說明糾纏態的手性開關確實對路徑參數的無序擾動表現出了魯棒性。

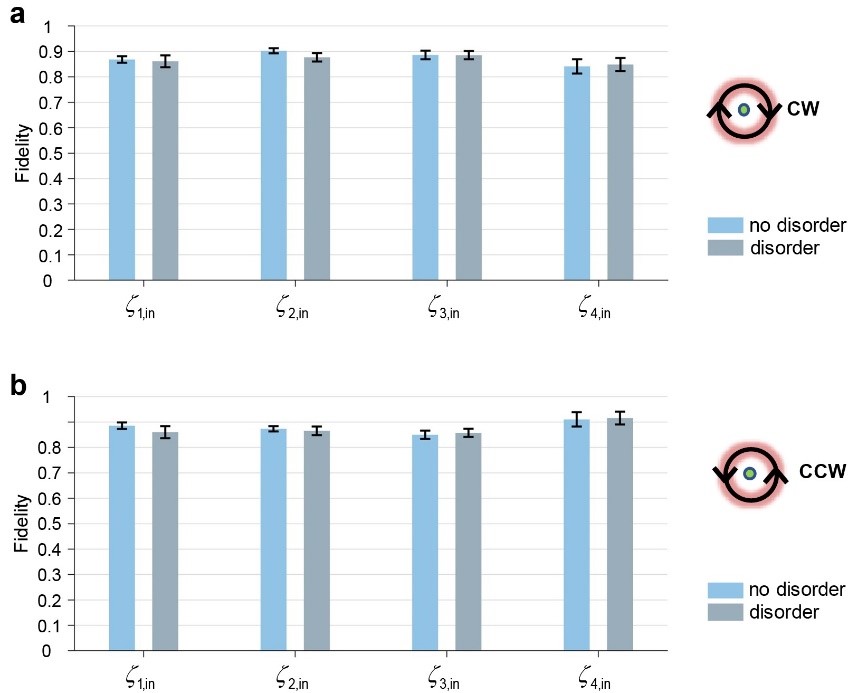
圖5. 量子糾纏態開關的魯棒性證明

實現糾纏態轉換的通常方法是精確操縱雙量子比特門，不同糾纏態之間的轉換需要構建不同的量子門。然而，這種操作不具備拓撲保護特性，容易受到環境影響而出現誤差。在這項工作中，研究團隊通過設計四階簡并奇異點，提供了實現量子糾纏態高保真穩定運行的有效方案。由于所設計的具有簡并性奇異點的黎曼能面與糾纏態具有相同的特征態，因此可以通過環繞奇異點來實現糾纏態之間的非對稱轉換。由于黎曼曲面結構的拓撲特性，這種對糾纏態的操縱是受拓撲保護的。此外，這些現象已經通過量子行走平臺的構建得到了實驗證明。

以上討論的重點是環繞奇異點的情況。最近的研究表明，手性態轉移可以在不包圍奇異點或靠近奇異點的情況下出現。事實上，研究團隊設計的拓撲保護糾纏開關也可以在不包圍奇異點或靠近奇異點的情況下工作。這意味著其揭示的現象更容易在各種實際系統中實現，這對未來的量子信息、計算和通信研究是非常有意義的。

論文鏈接：https://doi.org/10.1038/s41377-024-01514-1